Ma trận giao hoán
Bài toán:
1) Tìm tất cả các ma trận vuông thực cấp 3×3 giao hoán với ma trận
2) Với n là một số nguyên dương. Giải phương trình sau trong M3(R)
Xn=A
(Đề bài trích từ Kỷ yếu Olympic toán sinh viên Việt Nam 2013)
Lời giải:
1) Giả sử
là ma trận cần tìm, giao hoán với ma trận A .
Từ phương trình
AB=BA
ta suy ra
d=g=h=0,a=e=i,f=3b
Vậy ma trận B giao hoán với ma trận A sẽ có dạng
∀a,b,c∈R
2) Giả sử X là nghiệm của phương trình Xn=A .
Ta có:
AX=Xn.X=X.Xn=XA
Như vậy, X giao hoán với A .
Theo câu 1) suy ra
Ngoài ra, ta còn có
detXn=detA=0
Suy ra
detX=0
Từ đó, ta có
a=0
và
Khi đó
và
X3=O⇒Xk=O∀k≥3,k∈N
Kết luận: Với n=1 ta có X=A là một nghiệm của phương trình Xn=A .- Với
n≥2 thì ∄X∈M3(R) thoả Xn=A .
1) Tìm tất cả các ma trận vuông thực cấp
2) Với
(Đề bài trích từ Kỷ yếu Olympic toán sinh viên Việt Nam 2013)
Lời giải:
1) Giả sử là ma trận cần tìm, giao hoán với ma trận
Từ phương trình
Vậy ma trận
2) Giả sử
Ta có:
Như vậy,
Theo câu
Ngoài ra, ta còn có
Suy ra
Từ đó, ta có
Khi đó
Với n=1 ta cóX=A là một nghiệm của phương trìnhXn=A .- Với
n≥2 thì∄X∈M3(R) thoảXn=A .

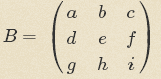




cảm ơn bạn
Trả lờiXóamình vẫn chưa hiểu :((
Trả lờiXóa